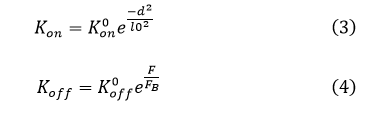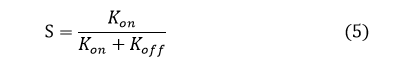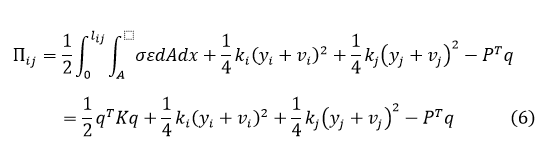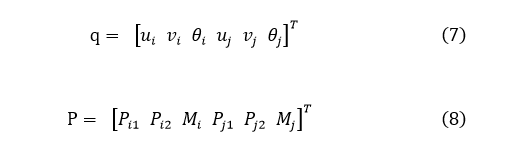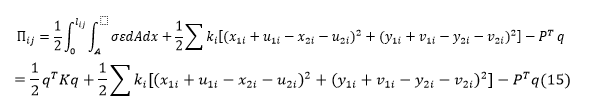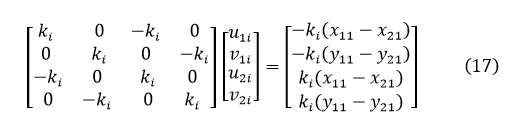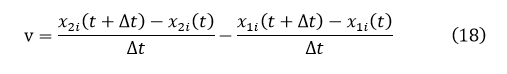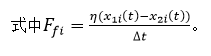薄膜黏附问题的有限元方法
薄膜黏附问题的有限元方法
上学期博主上了一门弹性力学变分课，变分的思想是泛函求极值，泛函是函数的函数。在运用中，可以把能量看作是一种泛函，能量（势能加外力功）是应力应变的函数，而应力应变又是位移和位移导数的函数，通过对能量求极值，得到数值解。而有限元方法正是通过这样的思想，求解模型。这次，博主使用有限元方法对薄膜的粘附问题进行求解，编程软件为matlab。
1. 背景和主要内容
在许多领域中，粘附和摩擦是一个非常普遍的现象，从微观到宏观，从生物到机器。因此粘附和摩擦具有很高的研究价值。近年来， 随着微纳米材料的发展与纳米尺度力学现象的深入研究，小尺度下的粘附和摩擦开始进入人们的视野。在众多的微纳米材料中，石墨烯材料是碳原子以六边形蜂巢晶格结构排列形成的平面薄膜，如图1所示，它的断裂强度比最好的钢材还要高100倍，与此同时它又很柔。石墨烯薄膜由于其出色的性能，具有十分广泛的应用前景，比如可用于制作各种电子设备。但在微纳米尺度下，电子器件中各组件的相互摩擦和粘附无法避免。而此类元件的表面积与体积之比很大，因此表面力成为可靠性设计时需考虑的主要载荷之一。本文的主要内容是使用变分原理得到了粘附段的刚度矩阵，结合多键合接触模型，引入粘附和摩擦对模型的影响。我们使用matlab软件编制模拟程序，并在对称RVE的粘附部分，使用此程序探究了石墨烯膜厚度与粘附长度的关系。最后，我们通过编写abaqus子程序vuinter来再次验证，但缺点在于abaqus的模型存在网格穿透的问题，目前还在解决中。
2. 多键合接触模型
多键合接触模型：用弹簧来描述表面间的接触，弹簧的形成和断裂代表两个接触面之间的相互作用。
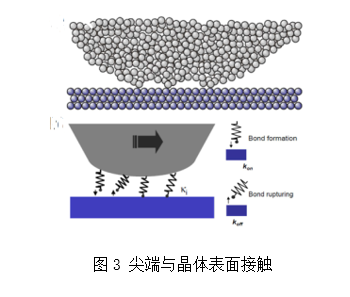
先介绍表面间的相互作用，图3模拟一个尖端与晶体表面的接触，即使尖端很小，也会与界面处形成多个接触[2]，接触的两个原子之间会形成相互作用力，当尖端远离表面时，相互作用力为拉力，阻止尖端运动，当尖端远离一定距离时，相互作用力消失。当靠近一定距离时，相互作用出现。这一过程与弹簧的形成与断开非常相似。
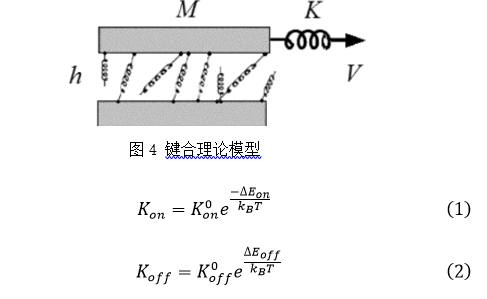
因此Filippov[3]多人提出一种键合理论的模型，如图4，通过弹簧连接两块刚性板，这些弹簧会自发断裂，然后在接触时重新形成。该模型中的动力学过程由两个相互竞争的过程控制：
（1）弹簧的形成，形成一个倾向于抑制滑动的连接
（2）弹簧的断裂，弹簧从其中一个板上分离，这一过程有助于滑动
形成速率Kon与断开速率Koff由相应的能垒决定，由公式（1）和（2）决定。
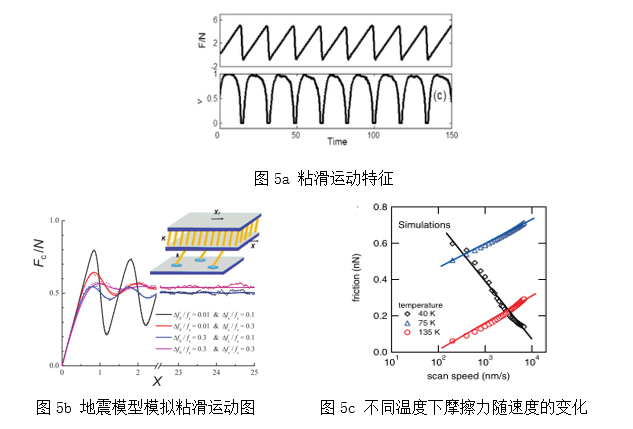
通过使用这个模型，Filippov[3]成功模拟出微观摩擦中的粘滑机制，如图5a。之后Braun[4]使用了类似的地震模型研究了出现粘滑运动的条件,如图5b。多接触模型还可以通过改变形成和断裂的速率，引入温度、速度对相互作用的影响，比如Barel[5]使用了类似的多接触模型，研究了温度对纳米摩擦的影响，如图5c。
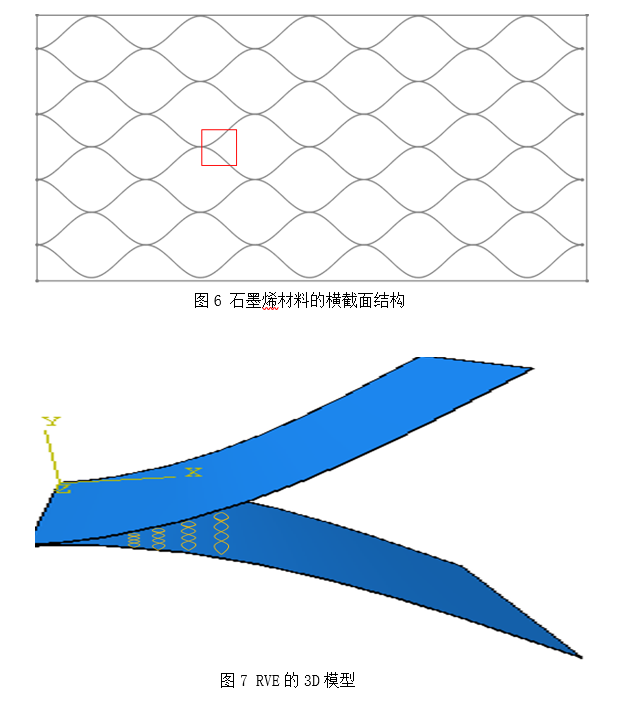
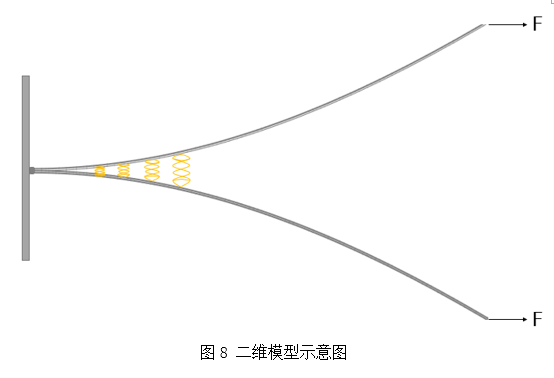
由于石墨烯膜之间的粘附是表面分子之间的相互作用，距离越远，相互作用越弱，反之，越强。因此采用多键合接触模型中多个键合的形成和断开来描述两个表面之间的相互作用。图6表示的是石墨烯膜材料的横截面结构示意图，我们对红色框里的RVE进行分析。图7是对称RVE的3D图，为了减少计算量，我们将对称RVE简化成二维图，如图8所示。
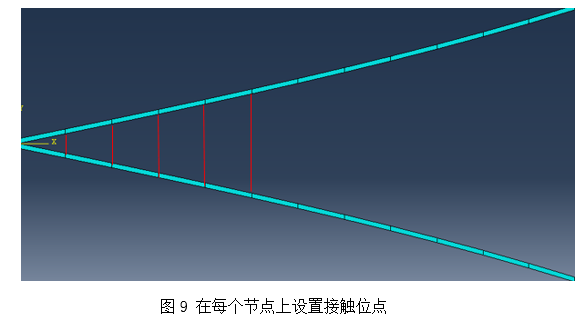
我们在有限元所划分节点上布置接触位点，如图9所示，在每一个接触位点上，我们假设有若干数目的接触，这些接触有两种状态：结合态（on）与断开态（off），两个状态之间可以相互转化，转速率分别为Kon、Koff，由公式（3）和（4）表示。我们将每一个接触位点上的接触数目归一化处理为相互作用强度，即当整个接触位点上所有的接触都处于结合态时，此位点上的表面相互作用强度（S）为1；反之，若所有接触都断开，则位点上的S为0.具体位点上接触的强度S由形成速率Kon与断开速率Koff两者共同决定。
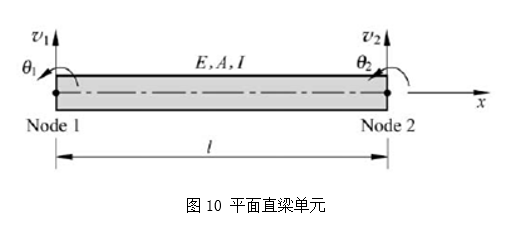
式中d为弹簧伸长长度，l0为特征长度，F为弹簧力，FB为特征弹簧力，Kon与Koff分别为接触形成与断开的特征速率。易知，在一段时间达到平衡后，表面相互作用强度值S如下所示,其取值范围为0-1：
3. 有限元方法
这里对结构划分的是平面直梁单元。平面直梁是指变形前轴线为直线、载荷位于其主形心惯性平面能的承弯构件[6]。如图10所示的局部坐标系内的梁单元，其长度为1，弹性模量为E，惯性矩为I，有两个节点，此直梁单元有6个自由度(DOF),其中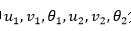
分别为两个节点的位移和转角。利用函数插值、几何方程、物理方程以及势能计算公式，可以将单元的所有力学参量用节点位移列阵及相关的插值函数来表示。
对于整个接触界面，并不是所有节点都会受到粘附力，相距较远的界面，其相互作用可近似忽略。因此整个界面分成粘附段和非粘附段，非粘附段的刚度矩阵为二维直梁单元矩阵，在这里不进行描述。而粘附段中编号为i,j两个节点确定的单元，易知其总势能表达式：
式中q为节点位移矩阵，其表达式为公式（7），P为节点外力矩阵，其表达式为公式（8），ki为i节点上的弹簧弹性系数，ki = kS（k为弹簧系数，S为表面相互作用强度），x,y为节点坐标，u,v分别为对应方向的位移。
将公式中的势能对节点位移矩阵q取变分，易得：
式中K’和P’的具体形式分别为：
其中T为坐标变换矩阵，
为局部坐标系下的二维直梁单元刚度矩阵，具体形式为
模拟所需的参数如下：
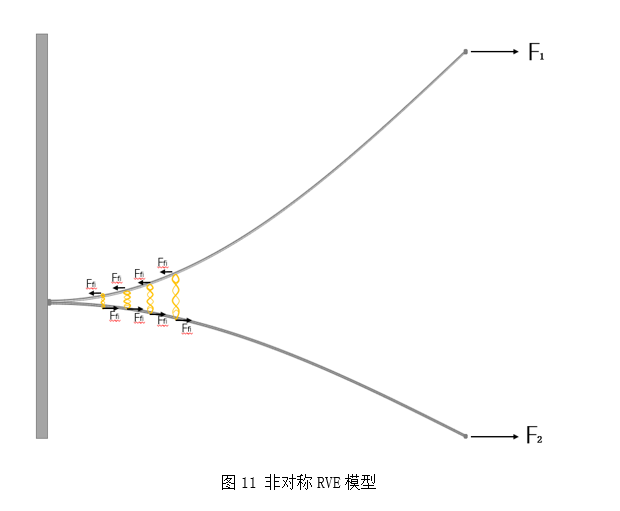
以上是在探究对称RVE单元的粘附作用，但在实际情况中，石墨烯薄膜大多不是对称的，如图11所示。而非对称的石墨烯薄膜层间会发生横向错动，导致层间摩擦，因此引入切向摩擦力是非常有必要的，切向摩擦力的公式如下：
上图非对称模型的总势能表达式为：
式中q为节点位移矩阵，K为无修正的总体刚度矩阵，ki为i节点上的弹簧弹性系数，ki = KS（k为弹簧系数，S为表面相互作用强度），x,y为节点坐标，u,v分别为对应方向的位移。式中位移矢量第一个下标1表示上层表面，2表示位于下层表面；第二个下标为节点编号。为了区分上下结构的刚度矩阵元素，用k表示位于上层，K表示位于下层。
将公式(15)中的势能对节点位移矩阵q取变分，得方程
式中K’为考虑弹簧修正后的总体刚度矩阵。界面上i节点上的弹簧平衡方程为：
最后我们采用显示格式计算相对速度v，其表达式如下：
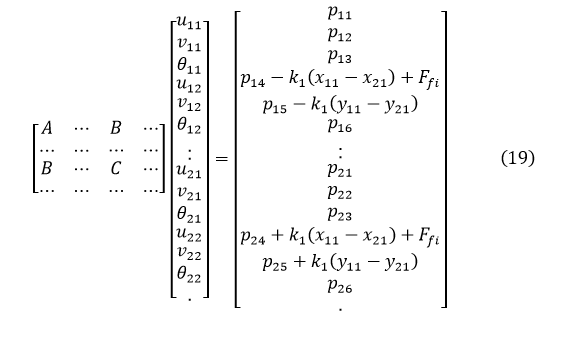
在有限元格式中，节点摩擦力可被看作集中载荷直接加到结构的总体方程中，经过调整，修正后的总体方程为：
其中：
根据以上公式，我们将单元刚度矩阵组集成整体刚度矩阵，并定义边界条件，代入材料参数。这里我们所求解的方法是使用matlab进行编程求解。
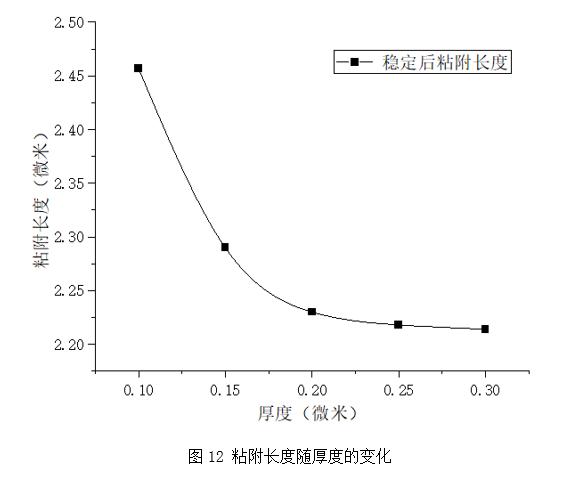
为了验证方法的可行性，在这里，我们测试了膜的厚度对粘附长度的影响。根据材料力学所学原理可知，厚度越厚，抗弯曲刚度越大，因此粘附段的长度就会减小。而厚度越小，结构抵抗变形的能力会降低，导致变形越大，增加了粘附长度。图12给出了粘附长度与厚度的关系。可以从图中看出，粘附长度随厚度的变化是非线性的，当厚度较大时，粘附长度不会发生变化，稳定在一个值内,而这个值接近于初始粘附长度。
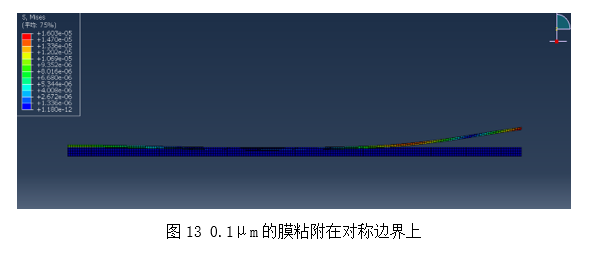
由于matlab编制的程序有较大的局限性，不能适应较为复杂的界面，因此我们还编制了abaqus的子程序vuinter，得到了厚度与粘附长度的关系，但是在abaqus中网格穿透的问题严重，目前还在解决中。
